Linear regression은 종속 변수 $y$와 한개 이상의 독립 변수 $X$와의 선형 관계를 모델링하는 방법론입니다. 여기서 독립 변수는 입력 값이나 원인을 나타내고, 종속 변수는 독립 변수에 의해 영향을 받는 변수입니다. 종속 변수는 보통 결과물을 나타냅니다.
선형 관계를 모델링한다는 것은 1차로 이루어진 직선을 구하는 것입니다. 우리의 데이터를 가장 잘 설명하는 최적의 직선을 찾아냄으로써 독립 변수와 종속 변수 사이의 관계를 도출해 내는 과정입니다.
$$f(x_i) = wx_i + b$$
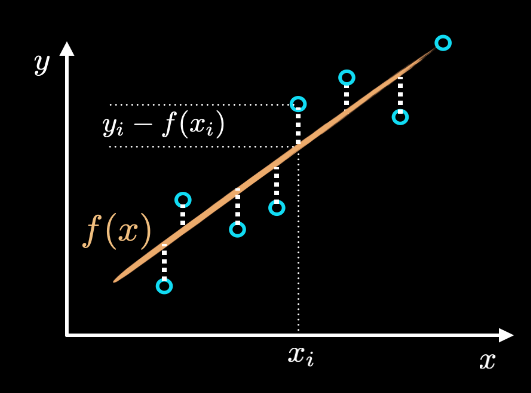
우리의 데이터를 가장 잘 설명하는 직선은 우리가 직선을 통해 예측한 값이 실제 데이터의 값과 가장 비슷해야 합니다. 우리의 모델이 예측한 값은 위에서 알 수 있듯 $f(x_i)$입니다. 그리고 실제 데이터는 $y$ 입니다.
실제 데이터(위 그림에서 빨간 점) 과 직선 사이의 차이를 줄이는 것이 우리의 목적입니다. 이 차이를 나타내는 것이 바로 cost function이고, 이를 바탕으로 cost function을 다음과 같이 정의해보겠습니다. (cost function은 loss function과 object function 라고 쓰기도 합니다.)
$$\text{cost function} = \frac{1}{N}\sum_{i=1}^n (y_i - f(x_i))^2$$
cost function은 이차함수입니다. 우리는 고등학교 수학시간에 이차함수의 최솟값을 구하는 방법을 배웠습니다! 고등학교 때 배웠던 방법을 다시 한번 알아보고, 새로운 gradient descent 방법도 알아보겠습니다.
예습
Analytically
다음 식의 최솟값을 어떻게 찾을 수 있을까요?
$$f(w) = w^2 + 3w -5$$
고등학교 때 배운 방법은 미분한 값이 0이 되는 지점을 찾는 것입니다.
sympy와 numpy 패키지를 사용하여 코드를 통해서 알아보도록 하겠습니다.
import sympy
import numpy
from matplotlib import pyplot
%matplotlib inline
sympy.init_printing()
w = sympy.Symbol('w', real=True)
f = w**2 + 3*w - 5해당식(2차 함수)의 그래프는 이렇게 생겼습니다.
sympy.plotting.plot(f);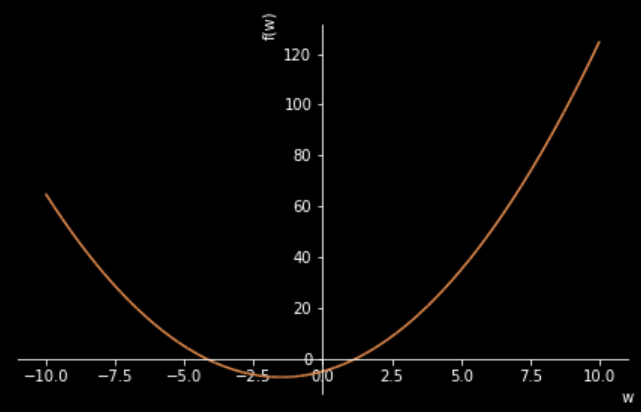
해당식을 미분해 보겠습니다.
fprime = f.diff(w)
print("결과 : ", fprime)결과 : $2w + 3$
그리고 해당 식의 해는 다음과 같이 구할 수 있습니다.
sympy.solve(fprime, w)
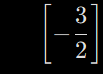
Gradient Descent 경사 하강법
두번째 방법은 Gradient Descent 방법으로 한 번에 정답에 접근하는 것이 아닌 반복적으로 정답에 가까워지는 방법입니다. Gradient Descent는 아래 그림과 같이 최솟값을 향해서 점점 다가가는 방법입니다. 이것도 코드를 통해서 이해해보도록 하겠습니다.
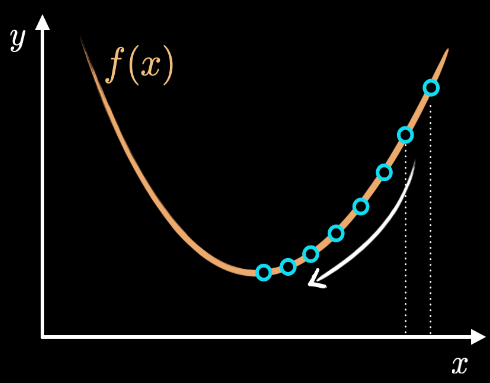
먼저 기울기 값을 구하는 함수를 만듭니다.
fpnum = sympy.lambdify(w, fprime)그 다음 처음 $w$ 값을 설정한 뒤, 반복적으로 최솟값을 햐해서 접근해보겠습니다.
w = 10.0 # starting guess for the min
for i in range(1000):
w = w - fpnum(w)*0.01 # with 0.01 the step size
print(w)
이처럼 첫번째 방법과 두번째 방법에서 같은 값이 나온 것을 알 수 있습니다.(-1.4999999980645... 와같은 근사치가 나온이유는 float형의 어쩔 수 없는 부동소수점 계산 오류에서 비롯된 것입니다. )
Linear regression 선형 회귀분석
실제로 linear 한 데이터 셋을 사용하기 위해서 가짜 데이터 셋을 만들어보도록 하겠습니다.
Numpy 패키지 안에 Normal distribution 함수를 통해서 조금의 noise 를 추가해서 100개의 데이터를 생성했습니다.
x_data = numpy.linspace(-5, 5, 100)
w_true = 2
b_true = 20
y_data = w_true*x_data + b_true + numpy.random.normal(size=len(x_data))
pyplot.scatter(x_data,y_data);
cost function을 나타내보면 다음과 같습니다.
w, b, x, y = sympy.symbols('w b x y')
cost_function = (w*x + b - y)**2Gradient descent 예시에서 한 것처럼 기울기 함수를 정의합니다.
grad_b = sympy.lambdify([w,b,x,y], cost_function.diff(b), 'numpy')
grad_w = sympy.lambdify([w,b,x,y], cost_function.diff(w), 'numpy')그리고 $w$와 $b$의 초기값을 정의하고 gradient descent 방법을 적용하여, cost function을 최소로 하는 $w$와 $b$값을 찾아보겠습니다.
w = 0
b = 0
for i in range(1000):
descent_b = numpy.sum(grad_b(w,b,x_data,y_data))/len(x_data)
descent_w = numpy.sum(grad_w(w,b,x_data,y_data))/len(x_data)
w = w - descent_w*0.01 # with 0.01 the step size
b = b - descent_b*0.01
print(w)
print(b)
처음에 데이터를 생성할 때 정의한, $w, b$ 값과 매우 유사한 값을 구할 수 있었습니다.
pyplot.scatter(x_data,y_data)
pyplot.plot(x_data, w*x_data + b, '-r');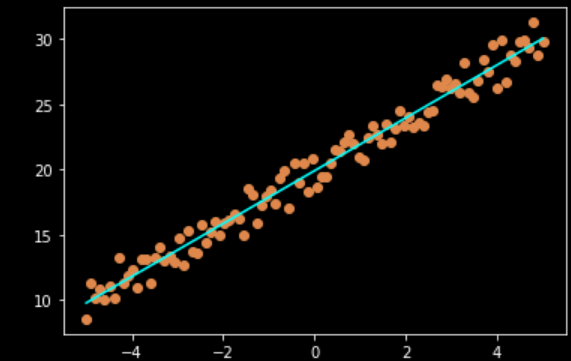
우리가 구한 직선이 데이터와 잘 맞는 것을 볼 수 있습니다.
실습
linear regression을 사용해서 시간 흐름에 따른 지구 온도 변화를 분석해보겠습니다.
Global temperature anomaly라는 지표를 통해서 분석을 해볼 것입니다.
여기서 temperature anomaly는 어떠한 기준 온도 값을 정해놓고 그것과의 차이를 나타낸 것입니다. 예를 들어서 temperature anomaly가 양수의 높은 값을 가진다면 그것은 평소보다 따듯한 기온을 가졌다는 말이고, 음수의 작은 값을 가진다면 그것은 평소보다 차가운 기온을 가졌다는 말입니다.
세계 여러 지역의 온도가 각각 다 다르기 때문에 global temperature anomaly를 사용해서 분석을 하도록 하겠습니다. 자세한 내용은 링크에서 확인하실 수 있습니다.
위 영상으로부터 기온이 점점 상승하고 있다는 것을 알 수 있습니다.
이제부터는 실제 데이터를 가져와서 분석해봅니다.
Step 1 : Read a data file
NOAA(National Oceanic and Atmospheric Administration) 홈페이지에서 데이터를 가져옵니다.
from urllib.request import urlretrieve
URL = 'http://go.gwu.edu/engcomp1data5?accessType=DOWNLOAD'
urlretrieve(URL, 'land_global_temperature_anomaly-1880-2016.csv')다운로드한 데이터를 numpy 패키지를 이용해 불러옵니다.
import numpy
fname = '/content/land_global_temperature_anomaly-1880-2016.csv'
year, temp_anomaly = numpy.loadtxt(fname, delimiter=',', skiprows=5, unpack=True)Step 2 : Plot the data
Matplotlib 패키지의 pyplot을 이용해 2D plot을 찍어봅니다.
from matplotlib import pyplot
%matplotlib inline
pyplot.plot(year, temp_anomaly);
Plot에 여러 정보를 추가해서 더 보기 좋게 출력합니다.
pyplot.rc('font', family='serif', size='18')
#You can set the size of the figure by doing:
pyplot.figure(figsize=(10,5))
#Plotting
pyplot.plot(year, temp_anomaly, color='#2929a3', linestyle='-', linewidth=1)
pyplot.title('Land global temperature anomalies. \n')
pyplot.xlabel('Year')
pyplot.ylabel('Land temperature anomaly [°C]')
pyplot.grid();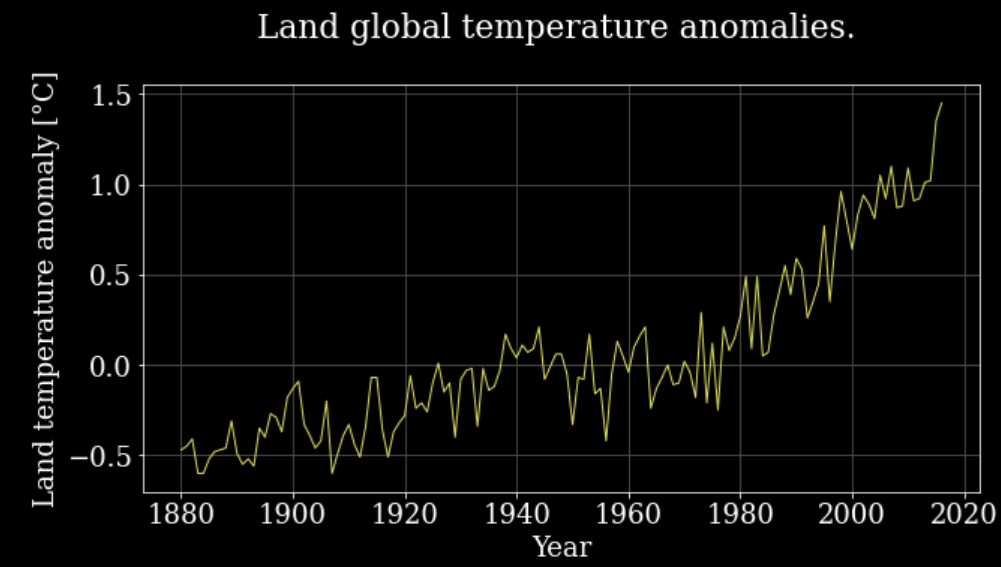
Step 3 : Analytically
Linear regression을 하기 위해서 먼저 직선을 정의합니다.
$$f(x_i) = wx + b$$
그 다음 cost function을 정의합니다. 우리가 최소화 해야 할 cost function은 다음과 같습니다.
$$\frac{1}{n} \sum_{i=1}^n (y_i - f(x_i))^2 = \frac{1}{n} \sum_{i=1}^n (y_i - (wx_i + b))^2$$
이제 cost function 을 구하고자 하는 변수로 미분한 뒤 0이 되도록 하는 값을 찾으면 됩니다.
먼저 $b$에 대해서 미분을 합니다.
$$\frac{\partial{J(w,b)}}{\partial{b}} = \frac{1}{n}\sum_{i=1}^n -2(y_i - (wx_i+b)) = \frac{2}{n}\left(b + w\sum_{i=1}^n x_i -\sum_{i=1}^n y_i\right) = 0$$
위 식을 만족하는 $b$에 대해서 정리하면
$$b = \bar{y} - w\bar{x}$$
여기서 $\bar{x} = \frac{\sum_{i=1}^n x_i}{n}$ , $\bar{y} = \frac{\sum_{i=1}^n y_i}{n}$ 입니다.
이제 $w$에 대해서 미분합니다.
$$\frac{\partial{J(w,b)}}{\partial{w}} = \frac{1}{n}\sum_{i=1}^n -2(y_i - (wx_i+b))x_i = \frac{2}{n}\left(b\sum_{i=1}^nx_i + w\sum_{i=1}^n x_i^2 - \sum_{i=1}^n x_iy_i\right)$$
여기에 아까 구한 $b$를 대입한 후 0이 되는 $w$값을 구하하면
$$w = \frac{\sum_{i=1}^ny_i(x_i-\bar{x_i})}{\sum_{i=1}^nx_i(x_i-\bar{x_i})}$$
가 됩니다.
우리는 계산을 통해서 $w$와 $b$ 값을 구했습니다.
이제 코드를 통해서 적용해봅니다.
w = numpy.sum(temp_anomaly*(year - year.mean())) / numpy.sum(year*(year - year.mean()))
b = a_0 = temp_anomaly.mean() - w*year.mean()
print(w)
print(b)0.01037028394347266
-20.148685384658464
이제 그래프로 그려서 확인해봅니다.
reg = b + w * year
pyplot.figure(figsize=(10, 5))
pyplot.plot(year, temp_anomaly, color='#2929a3', linestyle='-', linewidth=1, alpha=0.5)
pyplot.plot(year, reg, 'k--', linewidth=2, label='Linear regression')
pyplot.xlabel('Year')
pyplot.ylabel('Land temperature anomaly [°C]')
pyplot.legend(loc='best', fontsize=15)
pyplot.grid();
차트 위에 예쁘게 선이 그어진 것을 확인 할 수 있습니다.